[最も人気のある！] 三角比 求め方 円 476305-三角比 求め方 円

S＝rs となります 三角形の面積は，いろんな求め方がありますそこで， ヘロンの公式など を用いて三角形の面積を求めておくと，内接円の半径が求まります ヘロンの公式 三辺の長さが a , b , c である三角形の面積 S を求めるには まず、 s= ab平面図形 方べきの定理 説明 Date09年10月 1日 方 べきの 定理 とは， 平行でない 2本の直線と円とが交わって（接して）できる図形の辺の長さの関係 を示している公式です。 基本的には3つの形があります。 どれも三角形の相似から証明することができます。 ① 2つの直線の交点が円の内部にあるとき このとき， が成り立ちます。方べきの定理 方べきの定理はなぜ成り立つのか。 いずれのケースも、三角形の相似から説明されます。 1．点 \(p\) が円の内部にあるとき 円周角の定理から、下図の赤い角、ピンクの角がそれぞれ等しいため、 クリーム色の三

高校数学 円に内接する四角形の対角線の長さと面積 受験の月

三角比 求め方 円

三角比 求め方 円-・"球面上の最短距離は大円上で考える。" ・同経度の2地点間の距離を求めた。 ・"球面三角形は3つの大円の交わりから定義される。" ・（メネラウスの紹介） 1、球面上の「角」 角度について、『球面学』第1巻では以下のように定義している。弧の長さ は、 r θ と表されるので、中心角に比例します。 一方、 弦の長さ は、 2 r sin ⁡ θ 2 と表されるので、中心角には比例しません。 また、中心角が等しい場合、 弧の長さ は 弦の長さ よりも長いです。 どちらも、 0 ∘ ≤ θ ≤ 180 ∘ の範囲では

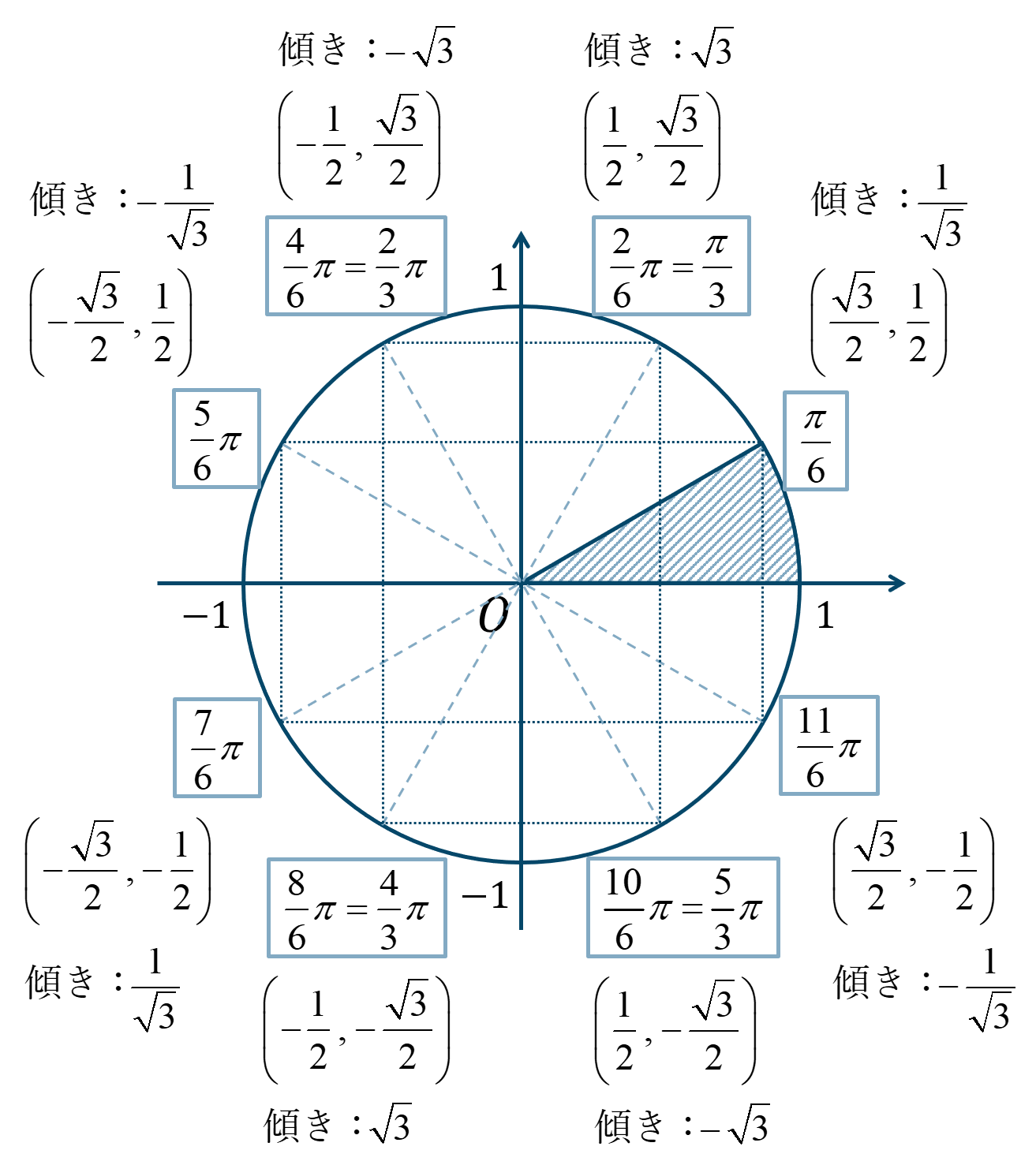
数学 単位円を用いた三角関数の値の求め方とコツ ページ 2 教科書より詳しい高校数学

92 Zeilenはじめに、単位円を用いた三角比の値の求め方を理解しておきましょう。 半径 \(1\) の円Sin , cos (サイン、コサイン）円を使った求め方 高1三角比・高2三角関数① 高校1年で習うサイン、コサイン（sin,cos)の値を円を用いて求めます。 sin (90°ーθ）＝cosθ ，cos (180°ーθ）＝ーcosθ もひとつひとつまある暗記している。 という状態でしたら、覚える負担が減りますし、テストなどで思い出す時の確認ができます。 まずは、単位円三角比 三角比の値の求め方数学苦手な人に向けて基本をイチから解説していくぞ！ 木の高さを三角比を用いて求める方法を解説！ 36°の三角比、二等辺三角形を用いて求める方法は？ sin75°、cos75°、tan75°の求め方！

三角比で円に内接する四角形の面積を求める手順 11 Step1 対角線をひき、余弦定理を使う 12 Step2 2つの三角形の面積の和を求める 13 ブラーマグプタの公式を使う 2 問題編四角形の面積を求めてみよう多数 (4～16個)の座標データから、円の直径が最小となる3点を見つけ、中心座標と直径を求めたい (エクセルで) アンケートにご協力頂き有り難うございました。 送信を完了しました。 三角形の外接円 のアンケート記入欄 性別 男 女 年齢 歳未満三角比2 正弦，余弦，正接をまとめて三角比という。 2 つの有な直角三角形を使います。今後，何度も 出てくる角度になりますので，右図を用いてすぐに 三角比を求められるようにしておきましょう。 仰角とは物を見上げたときの視線の方向と，

問2 図2の場合の三角比をX，Y で表せ。 sinθ= cosθ= tanθ= 問3 図3を見て次の問に答えよ。 (1)点Pの座標を求め，135 の三角比を求めよ。 P( , ) sin135 =cos135 = tan135 = (2)点Qの座標を求め，45 の三角比を求めよ。 Q( , ) sin45 =cos45 = tan45 =そうすると、右図3のように A と A' とが円に内接する四角形の向かい合う角になっているときは、 A'=180 °こんにちは、ウチダショウマです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こち

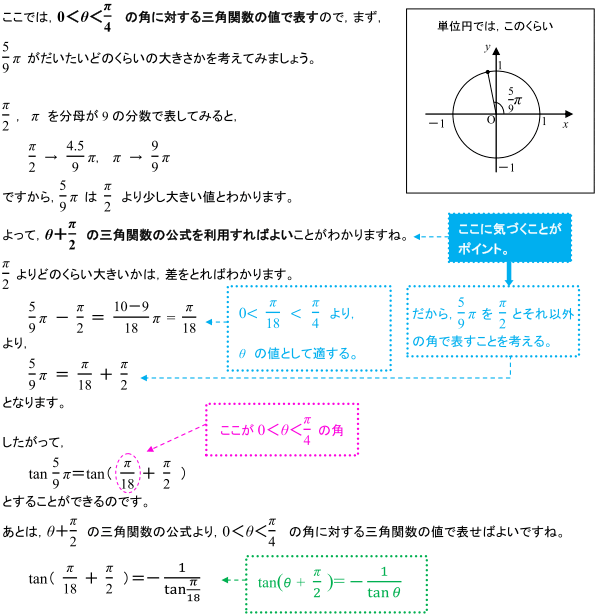
0 8 P 4 の角に対する三角関数での表し方 数学 苦手解決q A 進研ゼミ高校講座

8が90 の時のsinが1になりますが それを表した図を教えていただけると嬉しいです Clear

三角比の面積と円周率 ①円周率の正六角形の面積での近似 円周の長さで比較するより、「円の面積は内接正六角形の面積より大きく、外接正六角形の 面積より小さい」という比較の方が大小関係は明瞭でわかりやすいし、多角形の面積を求める 教材にも三角関数の合成 a \neq 0, b \neq 0 のとき、 \begin {align}a \sin\theta b \cos\theta = \sqrt {a^2 b^2} \sin (\theta \alpha)\end {align} ただし、 \begin {align}\displaystyle \cos\alpha = \frac {a} {\sqrt {a^2 b^2}}, \displaystyle \sin\alpha = \frac {b} {\sqrt {a^2 b^2}}\end {align}第4講「図形の計量」（3）空間図形への応用 「（佐藤の）数学教科書三角比・平面図形編」（東進ブックス）の学習 問43⊿ABCの3辺をa，b，c，面積をS，・・・外接円の半径をRとすると、次の関係が成立することを示しなさい。 （式1） S＝（abc）／（4R） 解答1 （解答おわり） この問題

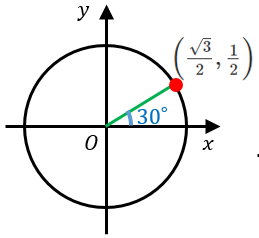
単位円を使った三角比の定義と有名角の値 0 180 具体例で学ぶ数学

48s96ub7b0z5f Net Sankakuhouteishiki Circle Graph

内接円の半径をｒとしたとき、３つに分けた三角形の面積は以下のように表すことができるんだ。 底辺ａ、高さｒ ➔1/2×ａ×ｒ 底辺ｂ、高さｒ ➔1/2×ｂ×ｒ 底辺ｃ、高さｒ ➔1/2×ｃ×ｒコラム 三角関数表（難易度2） 三角関数 は直角三角形に対して考えられる6種類の比の間の関係を扱う 三角法 がその起源で、角度に比の値を対応させる6種類の関数です。 三角法は英語ではtrigonometry といい、三角形の測量という意味です。 四千年前の三角形の面積比を使用しますが、 三角形の面積比の求め方には 高さが同じ三角形の場合や 相似な三角形の場合など、 いくつかパターンがあります。 その中で よく出題される1つの パターンについて お話をしていきます。 考え方を しっかりとマスターし

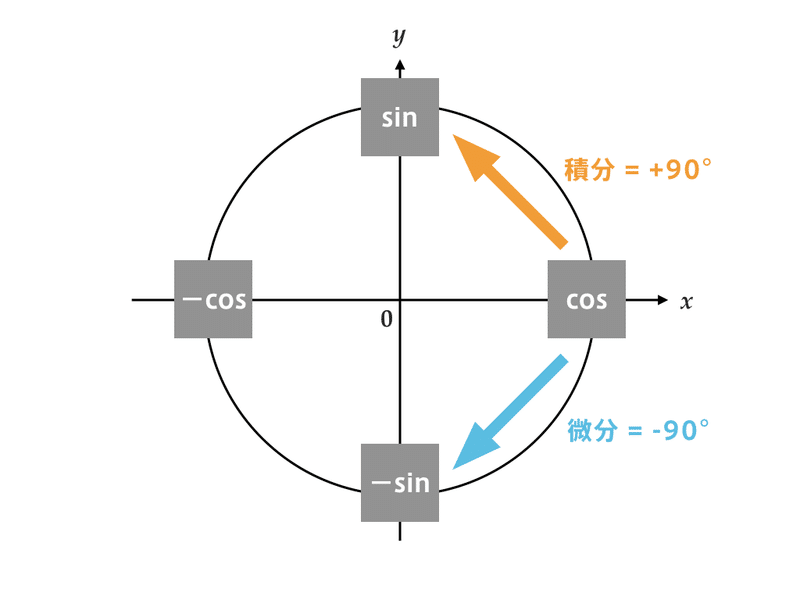
三角関数の微分 積分の覚え方 関谷 翔 Note

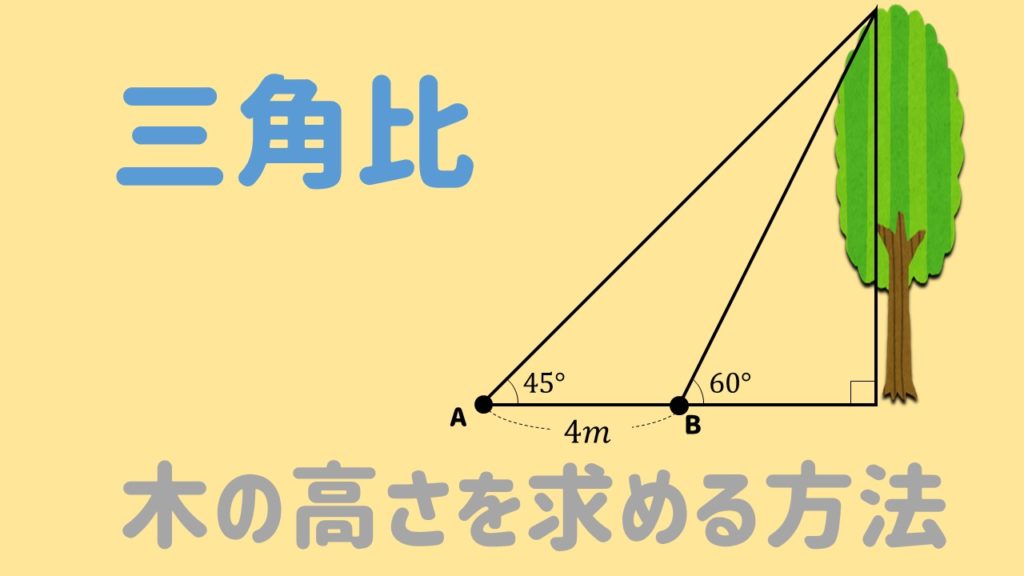
高1数学 木の高さを三角比を用いて求める方法を解説 数スタ

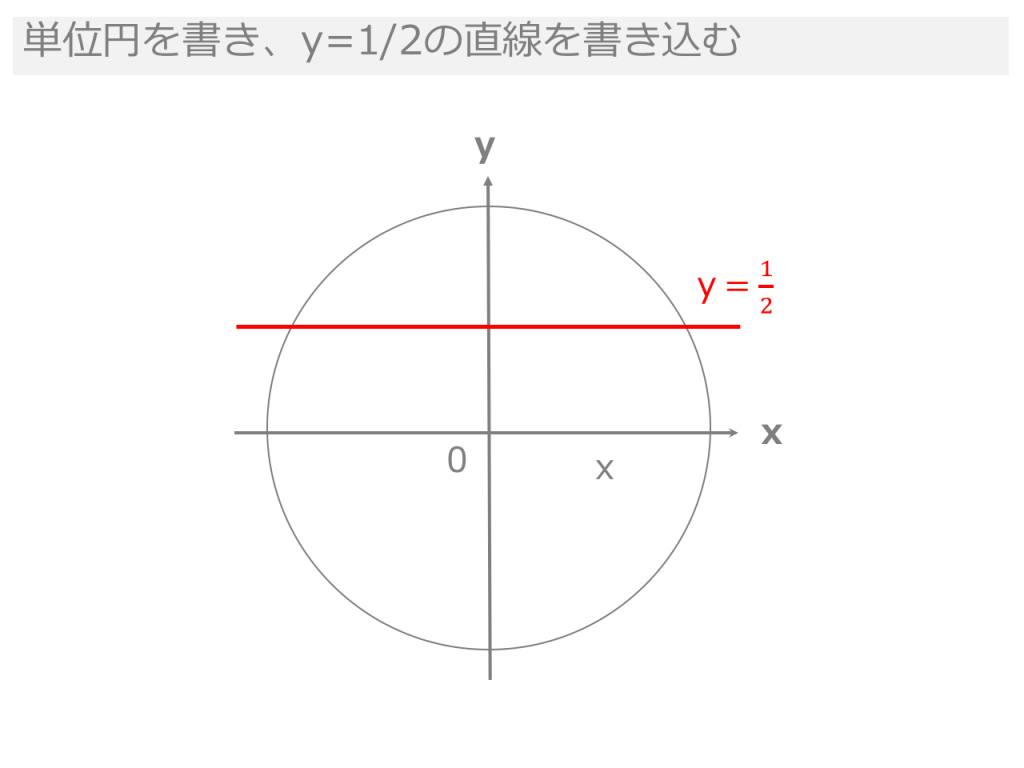
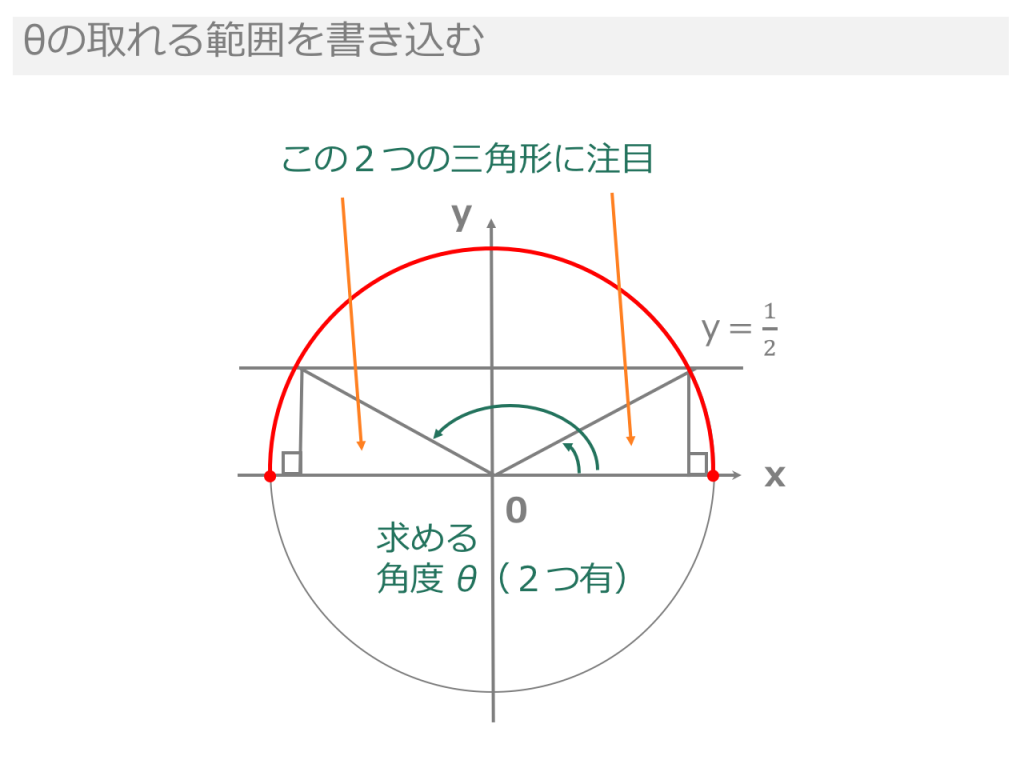
三角比を含む方程式を解くには、単位円（半径1の円）を使って考えるのが基本です。 三角比を含む方程式の考え方 \(\sin \theta =a\) ならば、 \(y=a\) の直線を引き、単位円との交点を求めて角度を求鈍角の三角比の求め方 解答左の図を見ながら，順を追って説明していきましょう。 ① 半円を描き，半径 (動く半径のことを 動径 と呼びます) を 1ﾟ 動かします。三角比の学 習意義と値 の求め方の 確認 ・始めに三角比とは，測量など，日常的な生活にも利用さ れている概念であったことを確認する。(5 分程度) ・プリント1 を配布し，表の空欄部分の値を埋めさせ

三角関数の公式 Sin Cos Tan と覚え方

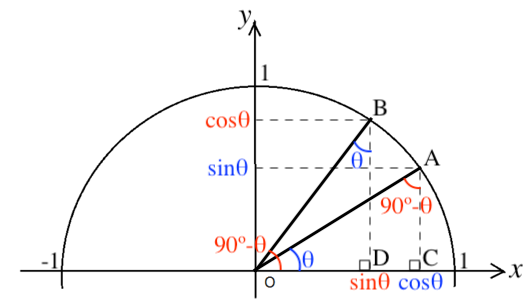
三角比の公式をしっかり理解しよう スタディクラブ情報局

三角比を用いた代表的な計算問題をマスターしましょう。この記事では「様々な三角比の四則演算」「等式を証明するもの」「sin, cos, tan の値を計算するもの」「式の値を計算するもの」についてまとめました。本記事で取り上げた問題はどれも定期試験頻出。三角形の内接円 の 正弦定理、余弦定理の求め方、三角形いろいろ「三角比の応用」 「第五公準、平行線問題とは何だったのか」なぜ証明出来なかったのか 「微積分とはどのような方法−A になりますので、 1を見ても分かるように sin A= sin A' が成り立ちます。 は に等しいので、 を求めてもよいことになります。

高校数学 内接円の半径の求め方 映像授業のtry It トライイット

要点 鈍角の三角比の値 Youtube

単位円から有名角の三角比を求める際の一覧表です！ お役に立てば幸いです🙇‍♂️ 学年 高校全学年, 単元 三角比, キーワード 数ⅰ,有名角,単位円,覚え方,三角関数のグラフ,sinのグラフ,数三角形における三角比の値 ABCでcosB の値を求めよ。 という問題で，cosB ＝3/2 と答えてしまいました。 sinθ ，cosθ ，tanθ の定義通りにあてはめたつもりですが，答えが正しくありませんでした。(高さ)÷2 底辺を x x ， 高さを y y とすると，三角形の面積 S S は次のように表せる． S = 1 2xy S = 1 2 x y

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

Sinとcosは何する関数 Creators Meetup Vol 22

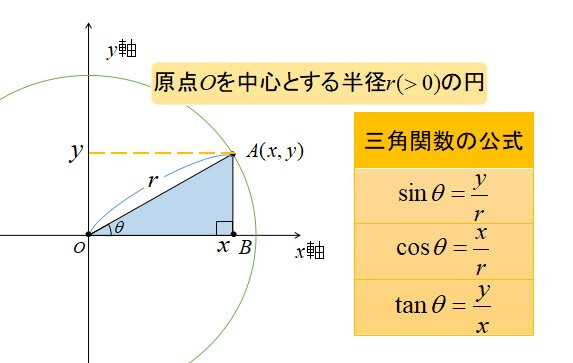
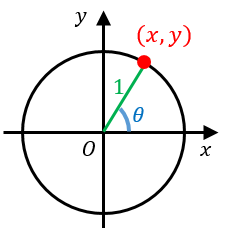
単位円で三角比を考える まずは復習です。実は単位円の考え方は三角比の範囲で少しやったことがあります。 どういうものだったかというと、まず座標平面上で半径が 1 の円である単位円を考えます。 この円上の点を一つとって原点と結びます。三角比におけるピタゴラスの定理のことですね。 図を書くと、右のようになります。 ＜先 生＞ 傾斜θの長さ1の斜辺を登るとき、水平方向、垂直方向の移動距離がそれぞれ、余弦、正弦の値だったよな。三角形（黒） 内接円 （青）と内心 (I) 傍接円（オレンジ）と傍心 (J A ,J B ,J C) 内角の二等分線（赤）と外角の二等分線（緑） 初等幾何学 において三角形の 内接円 （ないせつえん、 英 incircle / inscribed circle (of a triangle) ）とは、その 三角形 の内部にあり3

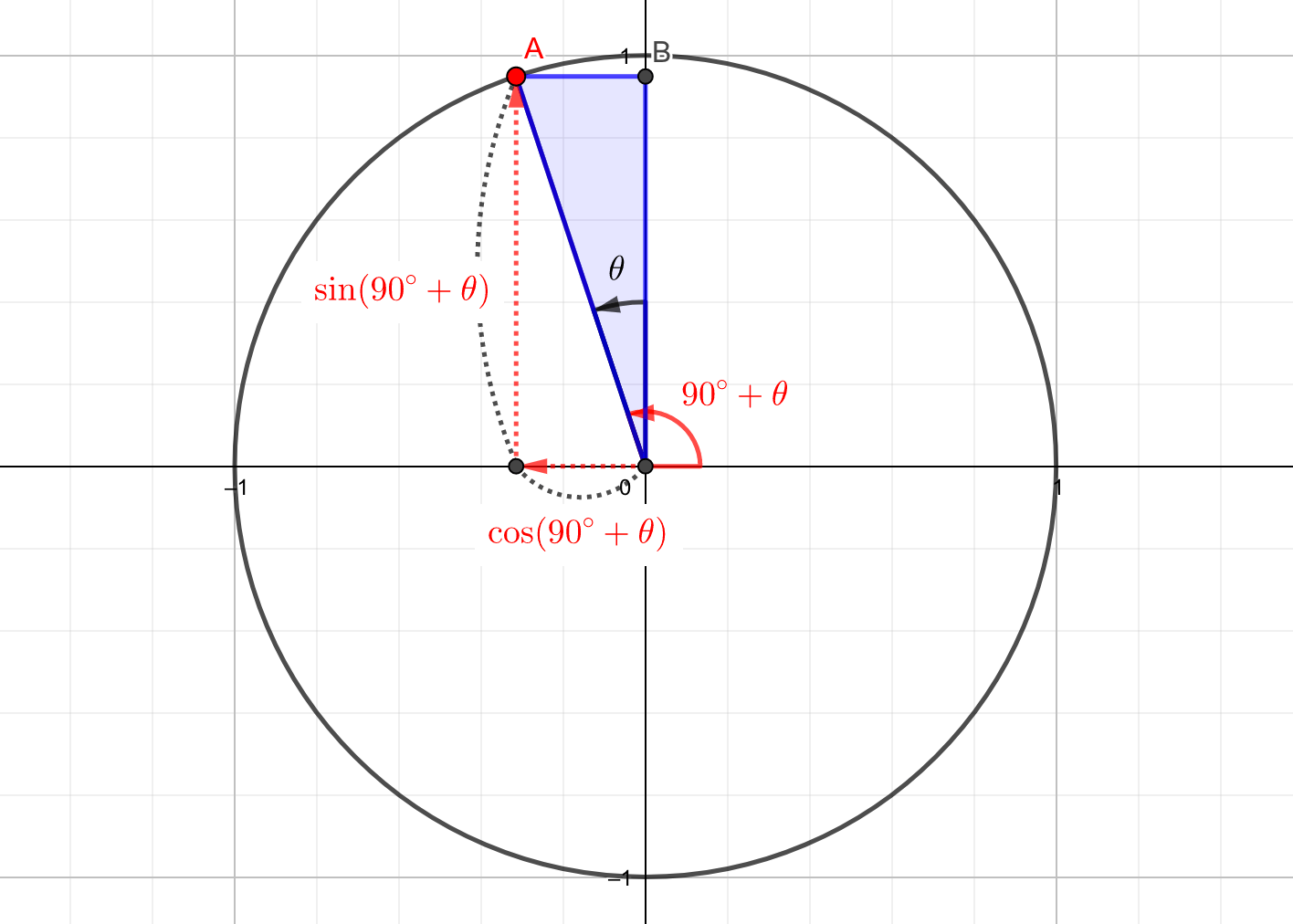
忘れても大丈夫 サインコサインの変換公式 覚え方とコツ 単位円を描こう 青春マスマティック

3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ

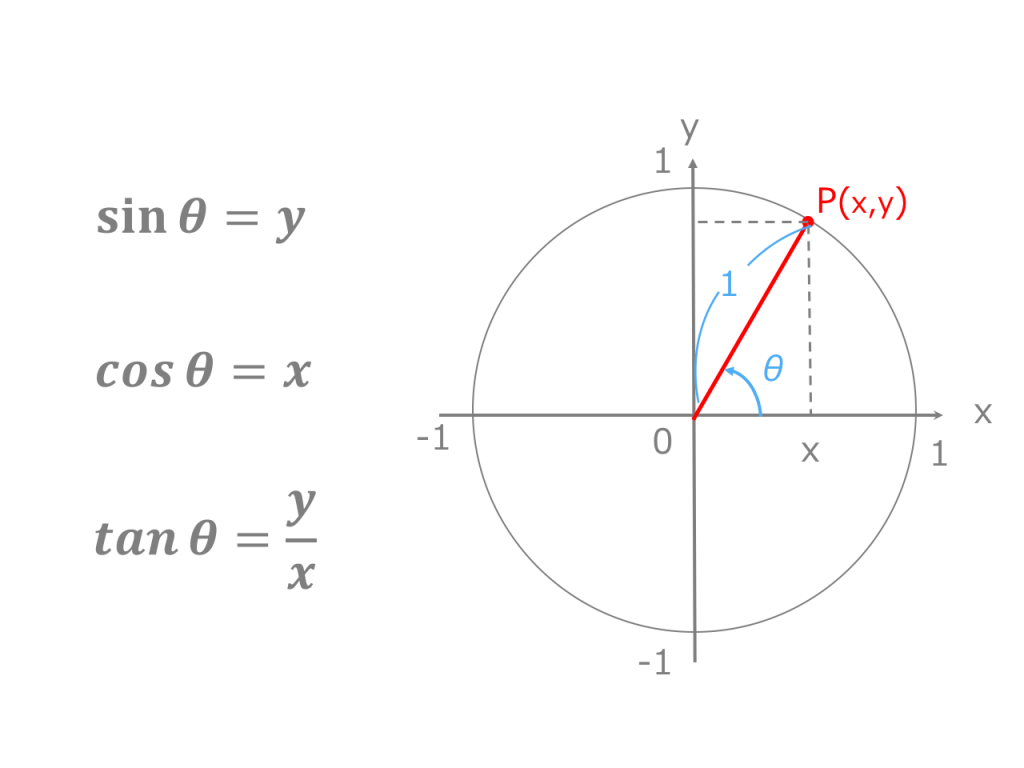
おわりに：三角形の外接円に関する公式=正弦定理を何よりも忘れない 正弦定理 と 余弦定理 。 三角比の範囲で必ず教わるような公式を使うことで、外接円の半径を求めることができます。前回 https//wwwyoutubecom/watch?v=hM_VhOlQeso&list=PLKRhhk0lEyzNXjYxLcVJBDQMnGQ9EJDEJ&index=41 次回 https//wwwyoutubecom/watch?v=3lobZKOa6OQ&index①、②とも三角関数の定義の単位円を思い出せば、簡単です。 ①は単位円の方程式がX 2 Y 2 =1だから、それにX=cosθ、Y=sinθを代入すれば出来ます。

3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

前回 https//wwwyoutubecom/watch?v=ZkUrV_xN4H8&index=8&list=PLKRhhk0lEyzOfDE8u9U0GWX3aa43XeMOr 次回 https//wwwyoutubecom/watch?v=5pEkPwf3Svo&index

数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ

数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ

単位円を使った三角比の定義と有名角の値 0 180 具体例で学ぶ数学

3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ

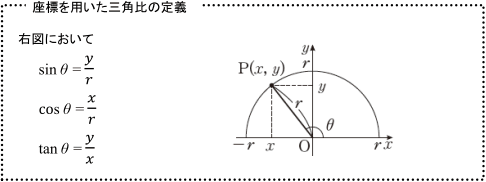
90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座

数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ

1

高1 三角比 数i 高校生 数学のノート Clear

三角関数の定義 鈍角の三角比を理解 完全に理解できます Rikeinvest

高1の数学iで 三角比の拡張の半円を使ったtan8の求め方がわかりません Yahoo 知恵袋

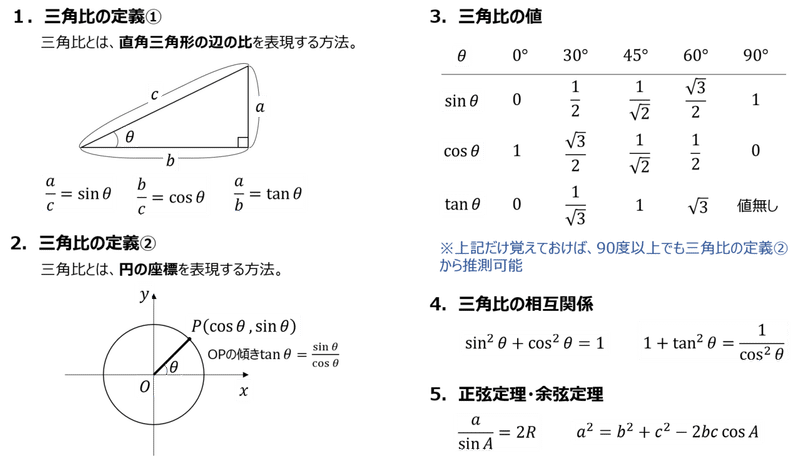
三角比は1時間で解けるようになる 箕輪 旭 Note

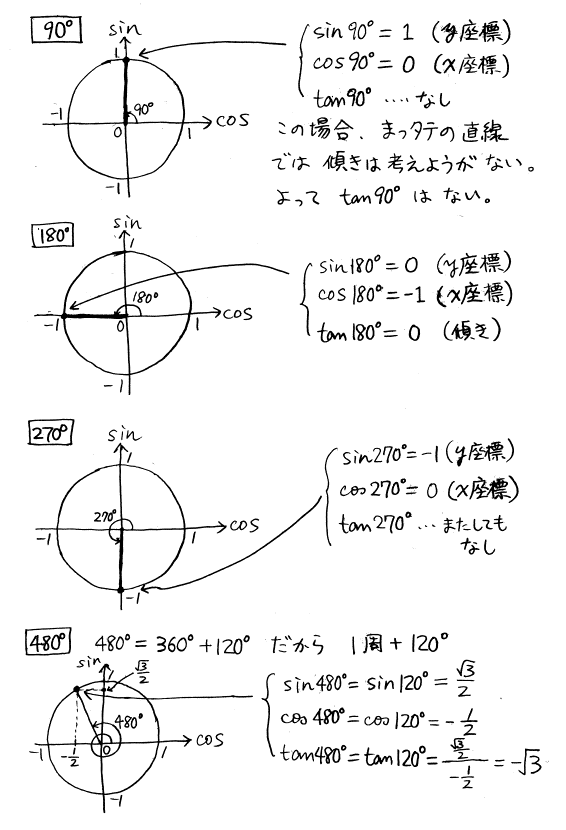
単位円と三角関数

Sin75度求め方 三角比 Pbhcl

三角関数の知識 やさしい電気回路

数 図形と方程式 補足 単位円 との関係 オンライン無料塾 ターンナップ Youtube

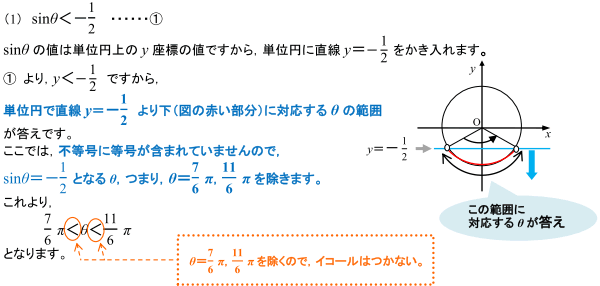
三角関数を含む不等式の解の求め方 数学 苦手解決q A 進研ゼミ高校講座

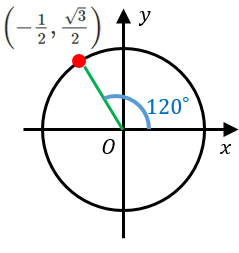
単位円を使った三角比の定義と有名角の値 0 180 具体例で学ぶ数学

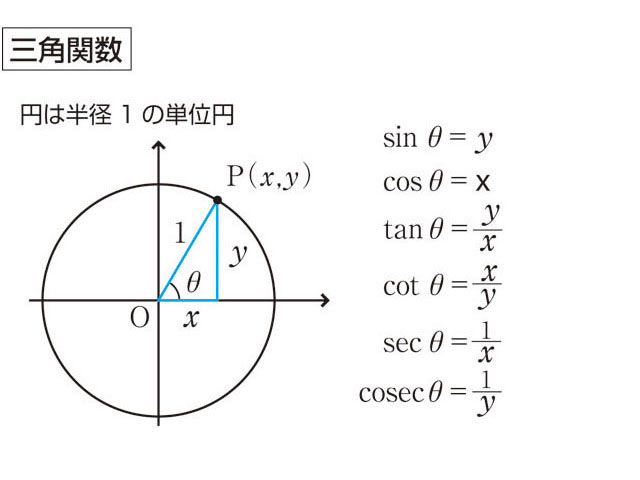
三角関数とは コトバンク

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

高校数学 三角比からの角度の求め方1 Sin8 例題編 映像授業のtry It トライイット

三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ

高校数学 三角比 使って覚える三角比の基本公式 数学の面白いこと 役に立つことをまとめたサイト

48s96ub7b0z5f Net Sankakukansuu Koushiki

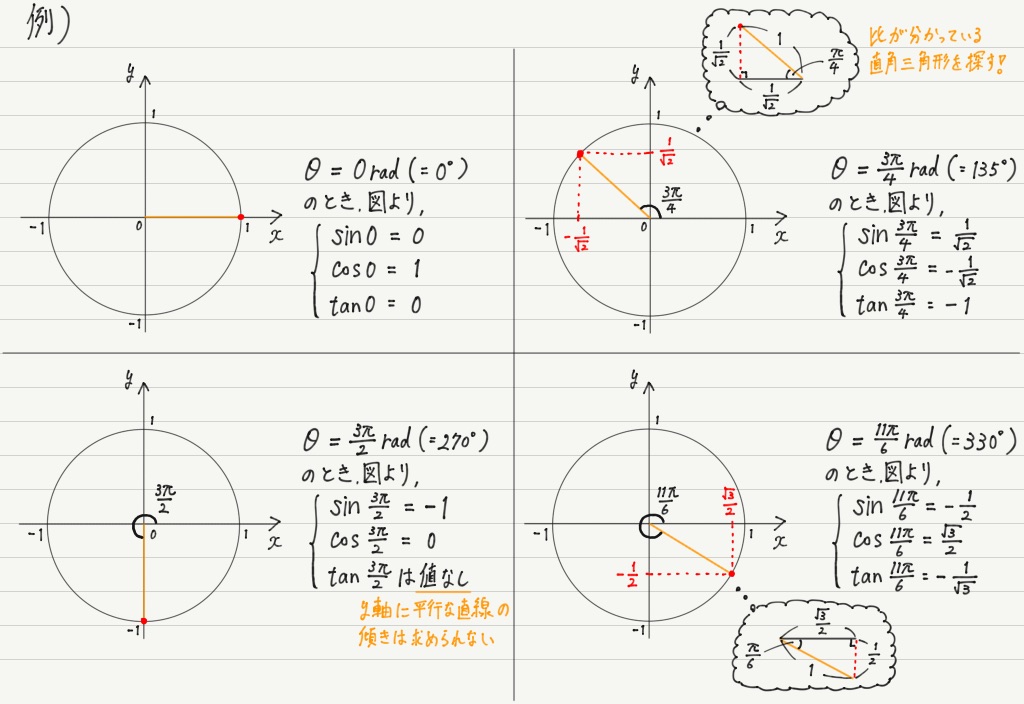
三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に

三角関数の基本 弧度法で表された8を用いてsin8 Cos8 Tan8の値を求める問題 数学ii By ふぇるまー マナペディア

三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ

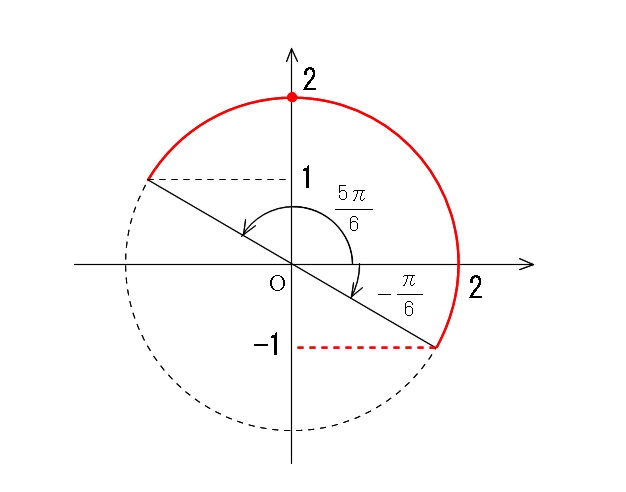
三角関数の合成と最大値最小値問題の解き方

ド文系が 三角比の拡張 と ラジアン をわかりやすく解説する

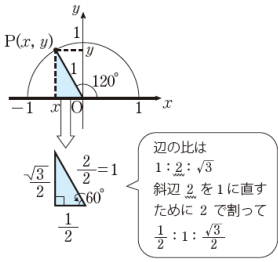
なぜ 点pの座標が分かるのでしょうか Clear

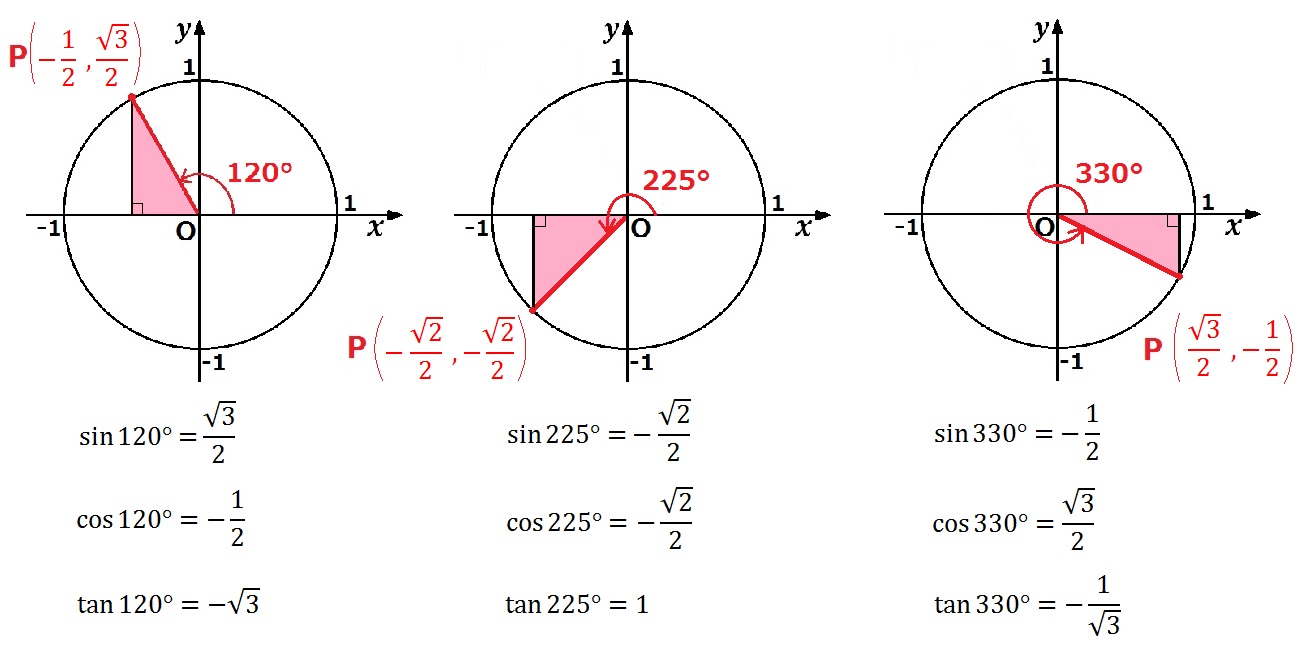
Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座

三角関数の知識 やさしい電気回路

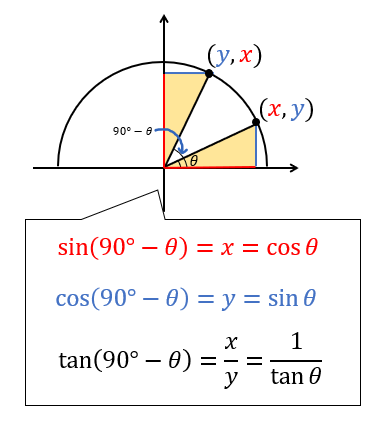
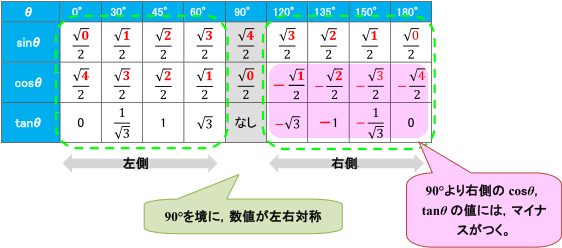
三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

高校数学 単位円を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 0 180 の三角比 受験の月

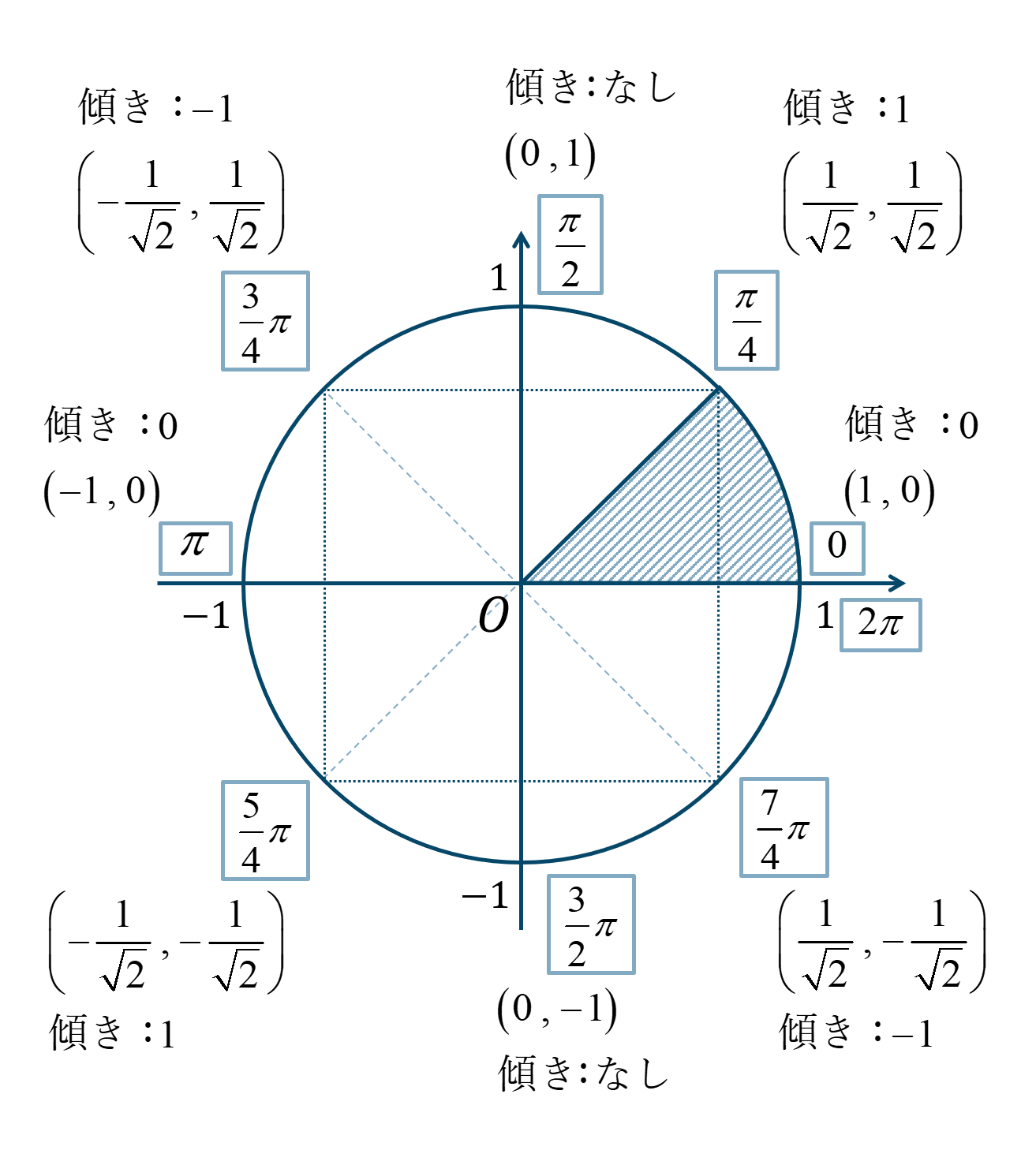
数学 問題演習 単位円を用いた三角関数の値 教科書より詳しい高校数学

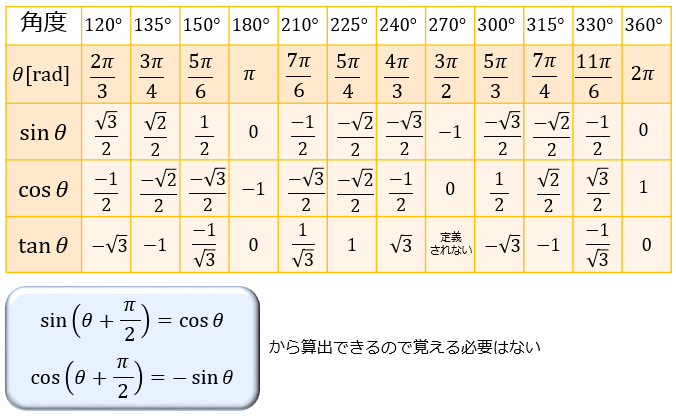
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

三角関数の値 Youtube

三角比を用いた計算問題をマスターしよう スタディクラブ情報局

タンジェント Tan の求め方を２つ 一歩一歩ぐんぐんブログ

数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ

48s96ub7b0z5f Net Sankakukansuu Seishitsu

三角比９ 単位円とその周辺 怜悧玲瓏 高校数学を天空から俯瞰する

1研究中 C 数学１ 三角関数 １ 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2

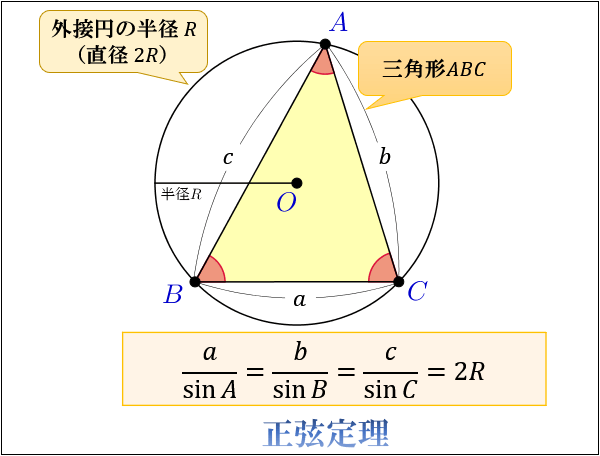
正弦定理とは何か 2つの視点から分かる公式の覚え方 考え方 アタリマエ

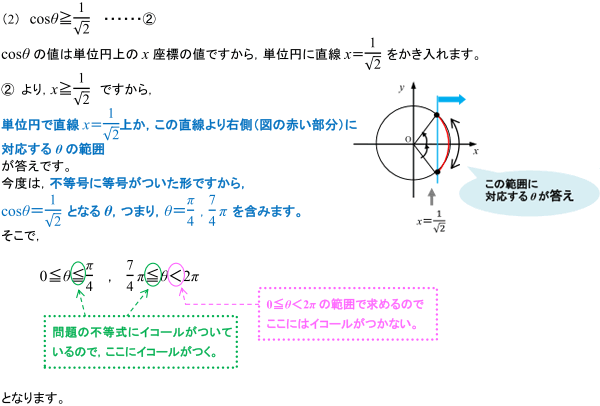
三角関数を含む不等式の解の求め方 数学 苦手解決q A 進研ゼミ高校講座

数学 単位円を用いた三角関数の値の求め方とコツ ページ 2 教科書より詳しい高校数学

高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット

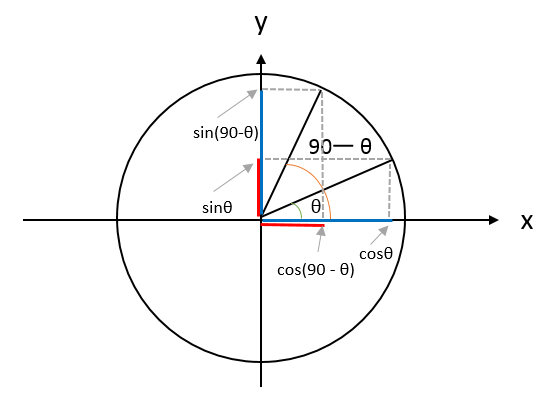
高校数学 余角 90 8 補角 180 8 の三角比公式を図で理解する 偏差値40プログラマー

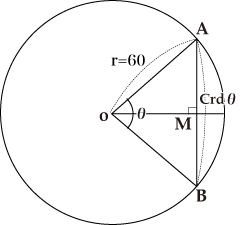
コラム 三角関数表 江戸の数学

3

高校数学 正弦定理と外接円 例題編 映像授業のtry It トライイット

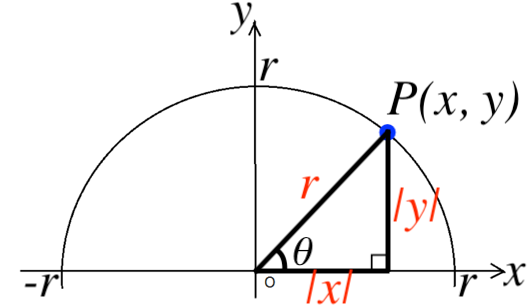
三角比の公式をしっかり理解しよう スタディクラブ情報局

有名角の三角関数は覚えるな 図から簡単に判断するコツ

1

サイン コサイン タンジェントの角度の求め方 一歩一歩ぐんぐんブログ

数学i 三角比 3 2 単位円周上の点の座標 Youtube

三角関数とは 1分でわかる意味 公式と計算 角度と値の関係

三角比の表 三角関数表 Sin Cos Tan の値 の一覧 受験辞典

90 8 180 8の三角比 Youtube

三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

Cos Sin Tanの有名角の表と簡単暗記方法 ビジュアル数学 数学１ 三角比 三角関数

三角関数の角度は 3分でわかる求め方 公式と計算 表との関係

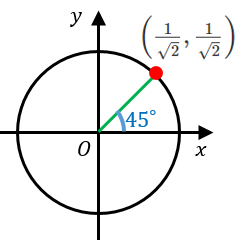
単位円を使った三角比の定義と有名角の値 0 180 具体例で学ぶ数学

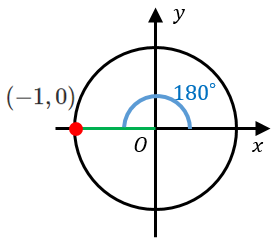
三角比 三角関数の公式を単位円と関連づけて理解する 関谷 翔 Note

三角関数を含む不等式の解き方と単位円を使うコツ

単位円を使った三角比の定義と有名角の値 0 180 具体例で学ぶ数学

三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

高校数 三角比 単位円 Sin Cos オンライン無料塾 ターンナップ Youtube

三角関数の公式の一覧 Wikipedia

標準 三角関数の値 なかけんの数学ノート

高校数学 数 ７６ 三角比 基本編 Youtube

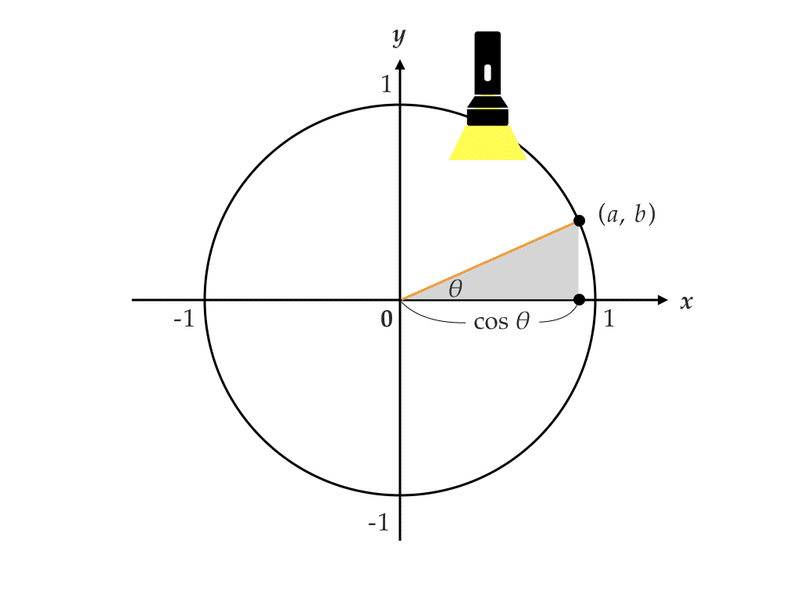
90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座

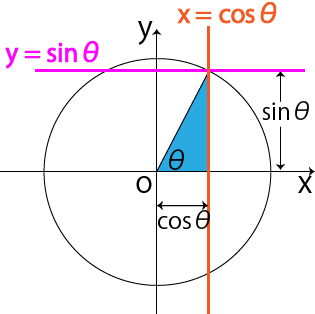
三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

高校数学 円に内接する四角形の対角線の長さと面積 受験の月

いろんな角度の三角関数を単位円で考える 高校数学の知識庫

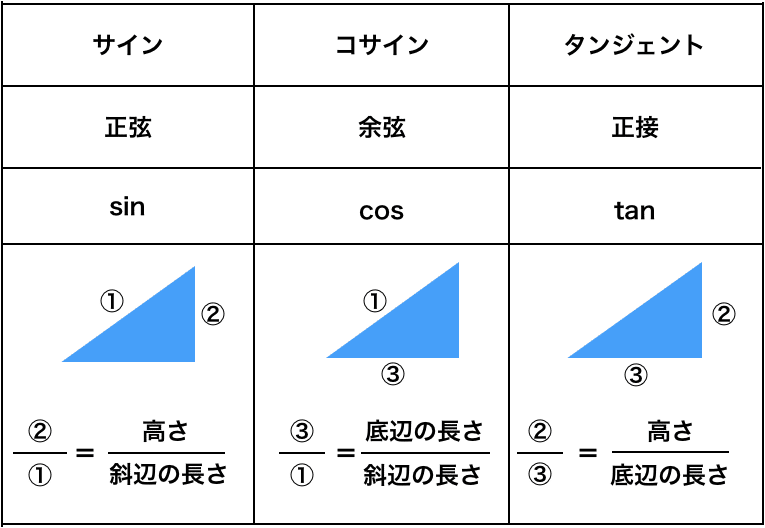
三角比の利用 Maekou Note

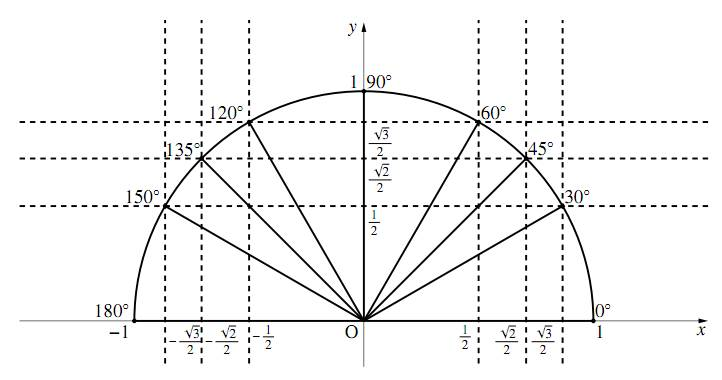
三角比の拡張 数学i フリー教材開発コミュニティ Ftext

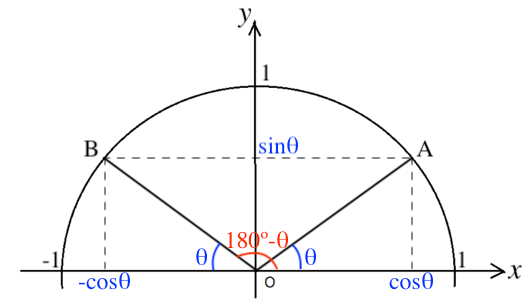
三角比の公式をしっかり理解しよう スタディクラブ情報局

1

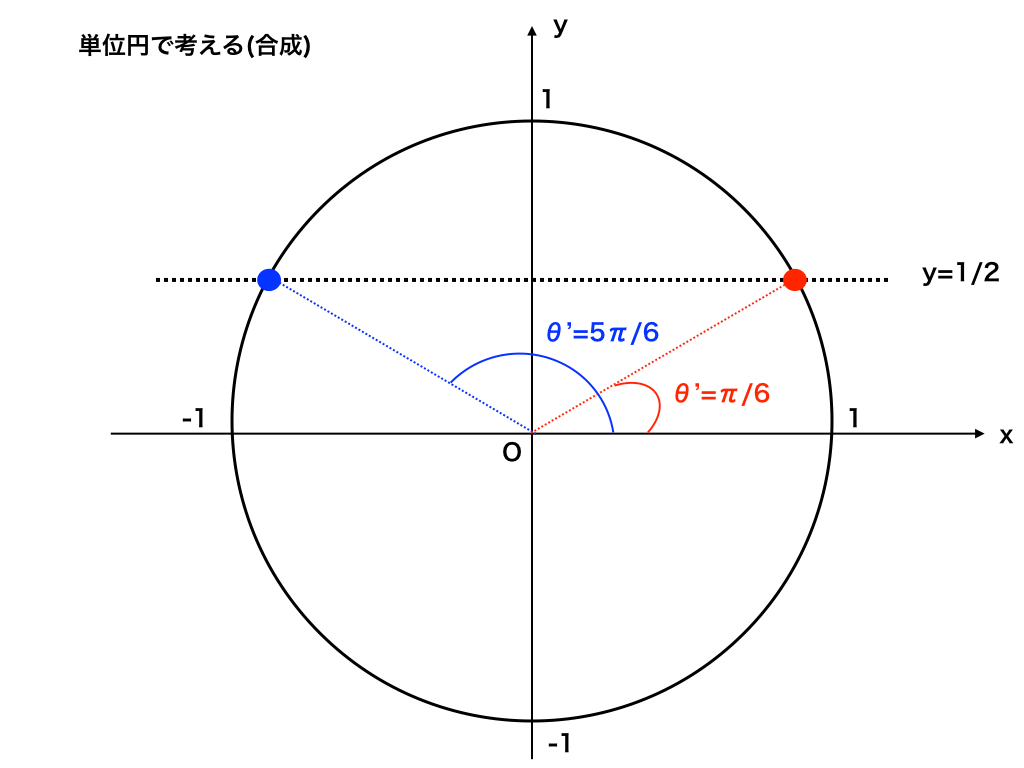
三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説

三角形の面積を外接円の半径を使って求める Schoolmath S Diary

三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

三角比の拡張

三角関数で角度から座標を導くふたつの式の使い途 Qiita

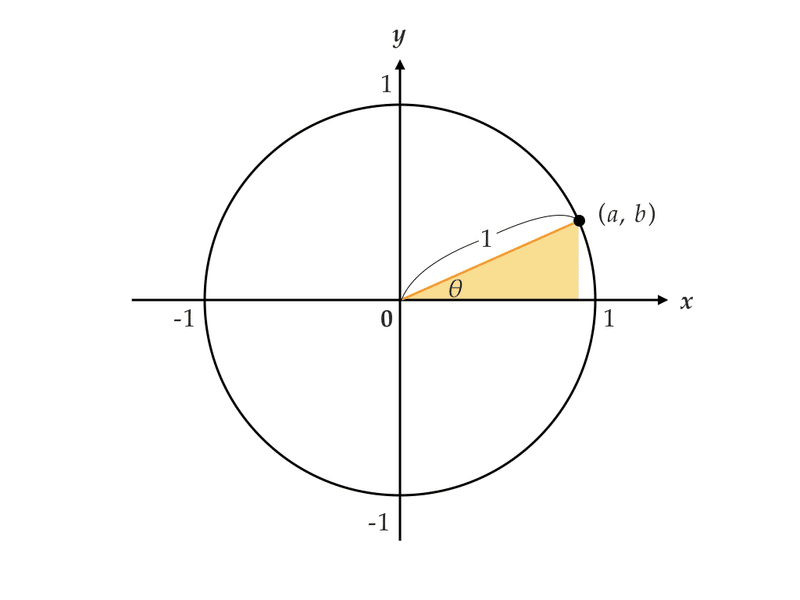
三角比 三角関数の公式を単位円と関連づけて理解する 関谷 翔 Note

三角 比 の 相互 関係 三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説 Amp Petmd Com

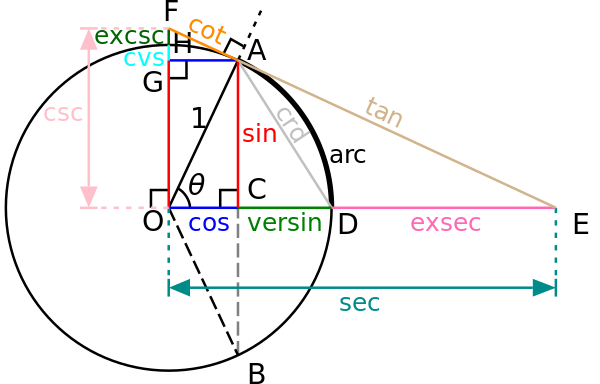
大学受験数学 三角関数 公式集 Wikibooks

Incoming Term: 三角比 求め方 円,